35 Contoh Soal dan Pembahasan Persamaan dan Pertidaksamaan Logaritma
 |
| 35 Contoh Soal dan Pembahasan Persamaan dan Pertidaksamaan Logaritma |
Persamaan dan Pertidaksamaan Logaritma adalah dua hal yang berbeda walaupun sama-sama berbicara tentang logaritma. Untuk memahami perbedaan antara persamaan dan pertidaksamaan logaritma, langsung saja simak ulasan-ulasan berikut.
Pengertian Persamaan Logaritma
Persamaan logaritma adalah suatu bentuk persamaan yang mengandung unsur/materi logaritma. Dibutuhkan kreatifitas yang tinggi untuk menyelesaikan persamaan logaritma. Tentu, sebelum berhadapan dengan persamaan logaritma, adik-adik sudah harus fasih dasar-dasar logaritma. Untuk memahami persamaan logaritma, langsung saja simak dan pelajari soal-soal berikut.
Contoh Soal
Pembahasan
syarat numerus
( ² + 4) (
² + 4) ( - 4) > 0
- 4) > 0
Jawab : b
2. Nilai  yang memenuhi persyaratan
yang memenuhi persyaratan =1+^{2}log\: x\; adalah......)
Pembahasan:
Ingat !!!
misalkan 2  =p
=p
p² - 2p - 3 = 0
(p + 1) (p - 3) = 0
p = -1 atau p = 3
Jawaban : b
d. 1
e. 2
Pembahasan:
2  = 1
= 1
Jawaban: c
4. Jika a > 0 maka penyelesaian dari .^{3}log\sqrt{a}=1) adalah.......
adalah.......
a. 1
b. 2
c. 3
d. 4
e. 5
Pembahasan:
ingat!!!
kalikan ruas kanan, dan ruas kiri dengan 2 sehingga:
2 + 1 = 9
+ 1 = 9
2  = 8
= 8
Jawaban: d
5. Hasil kali nilai X yang memenuhi persamaannya: =0) adalah.....
adalah.....
Pembahasan:
a. 144
b. 100
c. 72
d. 6
e. 5
Pembahasan:
modisifikasi persamaan logaritma menjadai:
= 144
Jawaban: a
6. Hasil kali akar-akar persamaan 
c. 1
d. 2
e. 3
Pembahasan:
persamaan logaritma menjadi
misalkan 
(p+5) (P-3) = 0
p = -5 atau p = 3
Jawab : a
7. Nilai yang memenuhi persamaan =log\; 10 \; adalah........)
a. -4
b. -3
c. -2
d. 3
e. 2
Pembahasan:
syarat basis
5 - 4  > 0 dan 5 - 4
> 0 dan 5 - 4 ≠ 1
≠ 1
(i). 5 - 4  > 0
> 0
5 > 4
(ii). 5 . 4 ≠ 1
≠ 1
5 - 1 ≠ 4
jadi syarat basis adalah 
Syarat noemerus:
( + 2) (
+ 2) ( - 5) = 0
- 5) = 0
tidak memenuhi syarat habis, karena syarat basis adalah  yang memenuhi syarat basis, adalah
yang memenuhi syarat basis, adalah
 = -2 priksa
= -2 priksa  = -2 dengan syarat numerus (-2)² - 7.(-2) - 5 = 13 > 0
= -2 dengan syarat numerus (-2)² - 7.(-2) - 5 = 13 > 0
Jawaban c
a. -4 atau 3
b. -3 atau 3
c. -2 atau 2
d. -1 atau 1





Pembahasan:
logaritma ruas kiri dan ruas kanan
ingat!!!
= 4
persamaan menjadi
Misalkan 
p² = 4
p² - 4 = 0
(p+2) (P-2) =0
p = -2 atau p = 2
kebalikan ke pemisaham
jawaban : d
8. Jika ^{\frac{1}{2}}-log\, 81^{x-5}=0) maka nilai x yang memenuhi persamaan itu adalah......
maka nilai x yang memenuhi persamaan itu adalah......
a. 14
b. 10
c. 8
d. 4
e. 2
Pembahasan:
Modisifikasi persamaan logaritma menjadi:
3 = 24
= 24
Jawaban = c
kita selesaikan dulu bagian
ingat !!
= 2.1
= 2
Sehingga

=2)




^{\frac{3}{2}})
^{2.\frac{3}{2}})
^{3})
 Jawaban: c
Jawaban: c





}=2)
.^{2}log\, x=2)
 p² + p - 2 = 0
p² + p - 2 = 0






1/3}log\, 3=^{5}log\, 3)
^{1/3}=5)
 = 41
= 41
^{2}-6(^{4}log\frac{x}{2})+1=0)
^{2}-6(^{4}logx-^{4}log2)+1=0)





^{log(x+1)}=\frac{(x+1)^{3}}{100})
.log(x+1)=log(x+1)^{3}-log100)
=3.log(x+1)-2)
=3.log(x+1)-2=0)
=1)

=2)

 Jawaban: c
Jawaban: c
15. Jika x memenuhi persamaan =^{x-2}log(4x+10)) dan a memenuhi a
dan a memenuhi a  = 7maka nilai a +
= 7maka nilai a +  = .......
= .......


persamaan logaritma menjadi
Ingat sifat-sifat logaritma jika
Sehingga
10. Jika  dan
dan  memenuhi persamaan
memenuhi persamaan }=2) maka nilai
maka nilai
 +
+  =........
=........
Pembahasan :
misalkan 
(p + 2) (p - 1) = 0
p = -2 atau p = 1
Jawaban : a
11. Nilai x yang memenuhi persamaan 
a. 42
b. 41
c. 39


Pembahasan:
3 = 123
= 123
Jawaban: b
12. Jika  dan
dan  memenuhi persamaan
memenuhi persamaan ^{2}-6(^{4}log\frac{x}{2})+1=0) maka
maka 
a. 3
b. 4
c. 6
d. 12
e. 20
Pembahasan:
misalkan 
2p² - 6p + 4 = 0
p² - 3p + 2 = 0
(p - 1) (p - 2) = 0
p = 1 atau p = 2
Jawaban: e
13. Jika  dan
dan  memenuhi persamaan memenuhi persamaan
memenuhi persamaan memenuhi persamaan ^{log(x+1)}=\frac{(x+1)^{3}}{100}) maka
maka

a. 81b. 96
c. 108
d. 120
e. 144
Pembahasan:
logaritmakan ruas kiri dan ruas kanan persamaan logaritma menjadi
^{log(x+1)}=log\frac{(x+1)^{3}}{100})
misalkan =p)
p² - 3p - 2 = 0
(p - 1) (p - 2) = 0
p = 1 atau p = 2
c. 6

=^{x-2}log(4x+10))





e. 8
Pembahasan:
syarat basis
syarat numerus
(i). 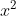 + 5 > 0 definitif positif selalu memenuhi untuk semua nilai
+ 5 > 0 definitif positif selalu memenuhi untuk semua nilai 
(ii). 4 > - 10
> - 10
persamaan
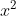 + 5 = 4
+ 5 = 4 + 10
+ 10 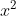 - 4
- 4 - 5 = 0
- 5 = 0
 = 5 atau
= 5 atau  = 1
= 1
 = 1 tidak memenuhi syarat basis adalah
= 1 tidak memenuhi syarat basis adalah  > 2 dan
> 2 dan  ≠ 3 yang memenuhi syarat basis adalah
≠ 3 yang memenuhi syarat basis adalah  = 5
= 5







( + 1) (
+ 1) ( - 5) = 0
- 5) = 0
a = 7
= 7
5a = 7
Jawaban: d
e. 4
Pembahasan :



=4) Ingat!!
Ingat!!


^{4})





 Persamaan
Persamaan=^{2}log\,4)
=2)



(x-1)=0)

 maka
maka  yang memenuhi syarat adalah
yang memenuhi syarat adalah  opsi yang benar adalah opsi 4
opsi yang benar adalah opsi 4

-^{4}log(4y^{2})=1) maka nilai p - q = ..........
maka nilai p - q = ..........

-^{4}log(4y^{2})=1)
=1)








+^{2}log(^{4}log\, x)=2) maka
maka  a. 1
a. 1
+^{2}log(^{4}log\, x)=2)
+^{2}log(\frac{1}{2}.^{2}log\, x)=2)
+^{2}log(\frac{1}{2}.^{2}log\, x)=2)
=^{2}log\, 4)

^{\frac{3}{2}}=8)
=8^{\frac{2}{3}})


 = 2⁴
= 2⁴ = 16
= 16











^{2})



 = 2 atau -2
= 2 atau -2
Jawaban: b
17. Nilai  yang memenuhi
yang memenuhi =^{2}log \,4 \: adalah.......)
b. 2.1
e. 2.1
Pembahasan:
syarat basis:
2 - 3 > 0 dan 2 - 3
> 0 dan 2 - 3 ≠ 1
≠ 1
Syarat numerus
memenuhi untuk semua nilai 
karena syarat basis adalah :
Jawaban: 4
18. Jika (p, q) merupakan penyelesaian dari sistem berikut,
a. 2
b. 4
c. 5
d. 9
e. 13
Pembahasan:
eliminasi pers * dan pers **
subtansi  = 9 ke pers *
= 9 ke pers *
p - q = 9 - 4 = 5
Jawaban : c
b. 2
c. 4
d. 5
e. 16
Pembahasan:
= 1
Jawaban: a
20. Jika  memenuhi persamaan
memenuhi persamaan 
a. 2 atau -2
c. 1 atau -1
d. 4 atau -4
Pembahasan :
yang ditanyakan adalah : 
Jawaban: a
Pengertian Pertidaksamaan Logaritma
Pertiadaksamaan logaritma adalah bentuk lain dari Persamaan Logaritma, dimana tanda "=" diganti dengan tanda" <, ≤, >, ≥". Untuk mempermudah pemahaman tentang pertidaksamaan logaritma, diharapkan adik-adik mempelajari kembali materi Pertidaksamaan. Ada keterkaitan yang sangat erat antara basis atau bilangan pokok logaritma dengan pertidaksamaan logaritma. Perhatikan rumus-rumus penting berikut !Rumus-Rumus Pertidaksamaan Logaritma
A. Untuk a < 0 < 1 dan f(x) > 0 dan g(x) > 0.1. Jika
2. Jika
3. Jika
4. Jika alog f(x) ≥  g(x) → f(x) ≤ g(x)
g(x) → f(x) ≤ g(x)
B. Untuk a > 1 dan f(x) > 0 dan g(x) > 0.
1. Jika f(x) <
f(x) <  g(x) → f(x) < g(x)
g(x) → f(x) < g(x)
2. Jika f(x) ≤
f(x) ≤  g(x) → f(x) ≤ g(x)
g(x) → f(x) ≤ g(x)
B. Untuk a > 1 dan f(x) > 0 dan g(x) > 0.
1. Jika
2. Jika
3. Jika  f(x) >
f(x) >  g(x) → f(x) > g(x)
g(x) → f(x) > g(x)
4. Jika f(x) ≥
f(x) ≥  g(x) → f(x) ≥ g(x)
g(x) → f(x) ≥ g(x)
Kadang-kadang kita membutuhkan pemisalan untuk menyelesaikan pertidaksamaan logaritma. Dengan pemisalan, kita bisa membuat pertidaksamaan logaritma menjadi lebih sederhana. Supaya adik-adik paham tentang pertidaksamaan logaritma, silahkan simak soal Pertidaksamaan logaritma berikut.
 yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan < 3\; adalah.........)
4. Jika
Kadang-kadang kita membutuhkan pemisalan untuk menyelesaikan pertidaksamaan logaritma. Dengan pemisalan, kita bisa membuat pertidaksamaan logaritma menjadi lebih sederhana. Supaya adik-adik paham tentang pertidaksamaan logaritma, silahkan simak soal Pertidaksamaan logaritma berikut.
Soal dan Pembahasan Pertidaksamaan Logaritma
21. Nilaisyarat numerus
2 > 3 > 0
> 3 > 0
2 > 3
> 3
syarat pertidaksamaan
karena bilangan pokok atau basis > 1 maka pertidaksamaan logaritma menjadi
2 - 3
- 3  8
8
2
 11
11
syarat basis sudah terpenuhi karena basis atau bilangan pokok adalah, 
syarat numerus
3 + 2 > 0
+ 2 > 0
3 > -2
> -2
syarat pertidaksamaan
karena basisnya adalah

^{-2})
(2)\to -\frac{2}{3}< x\leq \frac{7}{3})





< \; ^{3}log(2x-3))
 (
(  - 2) > 0
- 2) > 0 < 0 atau
< 0 atau  > 2 ................*
> 2 ................*

 ² - 2
² - 2 < 2
< 2 - 3
- 3 ² - 4
² - 4 + 3 < 0
+ 3 < 0
\bigcap(**)\bigcap (***)\to 2< x<0)





\geq ^{\frac{1}{2}}log(2x+3))
 (2
(2 -3) > 0
-3) > 0



 maka nilai
maka nilai
 yang memenuhi adalah..........
yang memenuhi adalah..........





+log\, 4) syarat numerus
syarat numerus > -3..............................**
> -3..............................**
.4)
 ² ≤ 4
² ≤ 4 + 12
+ 12 ² - 4
² - 4 - 12 < 0
- 12 < 0
\bigcap (**)\bigcap (***)\to 0< x\leq 6)

 > 0...................*
> 0...................*

}-\frac{p}{p(p-1)}-\frac{p(p-1)}{p(p-1)}< 0)
}> p^{2}-p+1)

 < 1 atau
< 1 atau  > 2.........................**
> 2.........................**
\bigcap (2)\to 0< x< 1\; atau\; x> 2)

 > 0 dan
> 0 dan  ≠ 1...................*
≠ 1...................*






\bigcap (**)\to \frac{1}{2}< x< 1\; atau\; x> 2)
< \; ^{\frac{1}{2}}log\, 81)
 syarat numerus
syarat numerus
< \; ^{\frac{1}{2}}log\, 81)
\bigcap (2)\to t< -3\; atau\; t> 0)






> 2)



 p (p + 2) > 0
p (p + 2) > 0

 Himpunan penyelesian:
Himpunan penyelesian:
 Jawaban: c
Jawaban: c






(p+1)< 0)


maka pertidaksamaan logaritma menjadi
Jawaban: d
23. Jika < ^{3}log(2x-3)) maka nilai
maka nilai  yang memenuhi adalah....
yang memenuhi adalah....
Pembahasan:
syarat basis sudah terpenuhi karena basisnya adalah 3 > 0 dan ≠ 1
syarat numerus
(i).  ² - 2
² - 2 dan ≠ 1
dan ≠ 1
(ii). 2 - 3 > 0
- 3 > 0
2 > 0
> 0
syarat pertidaksaaan karena basisnya adalah 3(a > 1), maka pertidakasamaan logaritma menjadi:
( -1) (
-1) ( - 3) < 0
- 3) < 0
1 <  < 3..................***
< 3..................***
24. Nilai x yang memenuhi pertidaksamaan: \geq ^{\frac{1}{2}}log(2x+3)) adalah.................
adalah.................
Pembahasan:
syarat basis
syarat basis sudah terpenuhi
syarat numerus
(i). 2 ² - 3
² - 3 > 0
> 0
(ii). 2 + 3 > 0
+ 3 > 0
2 > -3
> -3
syarat pertidaksamaan karena basisinya adalah ) maka pertidaksamaan logaritma menjadi
maka pertidaksamaan logaritma menjadi
2  ² - 3
² - 3 ≤ 2
≤ 2 + 3
+ 3
2 ² - 5
² - 5 - 3 ≤ 0
- 3 ≤ 0
(2 + 1)(
+ 1)( - 3) ≤ 0
- 3) ≤ 0
Jawab: e
a.  < 4
< 4
b. 0 < 
c. -2 <  < 16
< 16
d.  > 32
> 32
e.  < -4
< -4
Pembahasan:
Pembahasan:
\leq log(5x+10))
 > -2...................**
> -2...................** ² + 4
² + 4 + 4 ≤ 5
+ 4 ≤ 5 + 10
+ 10 ² -
² -  - 6 ≤ 0
- 6 ≤ 0
\bigcap (**)\bigcap (***)\to -2< x\leq 3)


syarat numerus
(i).  ² + 4
² + 4 + 4 > 0
+ 4 > 0
( + 2)² > 0→ selalu memenuhi jika
+ 2)² > 0→ selalu memenuhi jika  ≠ -2.................*
≠ -2.................*
(ii). 5 + 10 > 0
+ 10 > 0
5 > -10
> -10
syarat pertidaksamaan karena basis adalah 10 > 1, maka pertidaksamaan logaritma menjadi:
( + 2) (
+ 2) ( - 3) ≤ 0
- 3) ≤ 0
-2 ≤  ≤ 3....................***
≤ 3....................***
Jawaban: a
27. Himpunan penyelesaian pertidaksamaan +log\, 4) adalah............
adalah............
Pembahasan:
(i).  > 0 ....................*
> 0 ....................*
(ii).  + 3 > 0
+ 3 > 0
syarat pertidaksamaan
karena basis adalah 10 > 1 maka pertidaksamaan logaritma menjadi:
(  + 2) (
+ 2) ( - 6) ≤ 0
- 6) ≤ 0
-2 ≤  ≤ 6......................***
≤ 6......................***
Jawaban: c
28. Nilai yang memenuhi  adalah..............
adalah..............
a.  < 1 atau
< 1 atau  > 0
> 0
b. 1 <  < 2
< 2
c. 0 <  < 2
< 2
d.  < 2 atau
< 2 atau  > 3
> 3
e. 0 <  < 1 atau
< 1 atau  > 2
> 2
Pembahasan:
syarat numerus
misalkan 
definitif positif, bisa diabaikan ingat jika a > 0 dan D < 0 disebut depinitif positif
p (p - 1) > 0
p < 0 atau p >1
Jawaban: e
29. Nilai-nilai x yang memenuhi  adalah..............
adalah..............
a.  > 2
> 2
b.  > 1
> 1
d. -1 <  < 0 atau
< 0 atau  > 1
> 1
e. 1 <  < 2
< 2
Pembahasan:

syarat basis dan numerus
misalkan 
(p + 1) p (p - 1) > 0
Jawaban: c
30. Nilai-nilai yang memenuhi : < \; ^{\frac{1}{2}}log\,81) adalah.............
adalah.............
a. t < 3
b. -3 < t < 3
c. 0 < t < 3
d. -3 < t < 0
e. t < -3 atau t > 0
Pembahasan:
t⁴ > 0
selalu memenuhi untuk t ≠ 0 ....................*
t⁴ > 81
t⁴ - 81 > 0
(t² + 9) (t² -9) > 0
t² + 9 definitip positif
(t² - 9) > 0
(t + 3) (t - 3) > 0
t < -3 atau t > 3.......................**
Jawaban: e
31. Himpunan penyelesaian pertidaksamaan  adalah............
adalah............
Pembahasan:
p < -2 atau p > 0
32. Himpunan penyelesaian dari pertidaksamaan  dengan a > 1 adalah.......
dengan a > 1 adalah.......
Pembahasan:
Misalkan 
Jawaban: a
33. Himpunan penyelesaian pertidaksamaan ^{2}-^{a}log\, x-2> 2) dengan 0 < a < 1 adalah.......
dengan 0 < a < 1 adalah.......
Pembahasan:
misalkan 
^{2}-^{a}log\, x-2> 0)

(p-2)> 0)



0 < a < 1
atau
Jawaban: a







